How Do You Find The Sample Size In A Population Variance

You can easily calculate population or sample variance and standard divergence, as well as skewness, kurtosis, and other measures, using the Descriptive Statistics Excel Calculator.

Variance and Standard Deviation Definition and Adding

Variance and standard deviation are widely used measures of dispersion of information or, in finance and investing, measures of volatility of asset prices.

Variance is defined and calculated as the boilerplate squared deviation from the mean. Standard departure is calculated as the square root of variance or in full definition, standard deviation is the foursquare root of the average squared difference from the mean.

These definitions may sound disruptive when encountered for the first time. For detailed explanation how to calculate both measures encounter Computing Variance and Standard Deviation in four Like shooting fish in a barrel Steps.

Describing vs. Forecasting in Statistics

In general statistics performs 2 principal tasks. Its goal is either to draw something that has already happened or already exists (descriptive statistics), or to estimate something that has not happened yet or is not fully known (inferential statistics).

Descriptive statistics deals with the problem how to effectively await at data we already have. Inferential statistics (the estimating and forecasting office of statistics) deals with the problem of not having all the data.

Of these two wide areas of statistics, inferential statistics is the i that is much more than interesting and much more frequently used in finance and investing. After all, every bit investors or speculators, nosotros often have to face up the problem that we want to know what nosotros don't know (for example, whether stock XYZ will go up or downwards tomorrow and past how much).

Population vs. Sample

The primary task of inferential statistics (or estimating or forecasting) is making an opinion almost something by using only an incomplete sample of information.

In statistics it is very of import to distinguish betwixt population and sample. A population is defined as all members (e.g. occurrences, prices, almanac returns) of a specified group. Population is the whole group.

A sample is a part of a population that is used to describe the characteristics (e.g. mean or standard difference) of the whole population. The size of a sample can be less than 1%, or 10%, or 60% of the population, but it is never the whole population.

Population vs. Sample Variance and Standard Deviation

When calculating variance and standard deviation, it is important to know whether we are calculating them for the whole population using all the information, or nosotros are calculation them using just a sample of data. In the first case nosotros call them population variance and population standard deviation. In the 2d case we telephone call them sample variance and sample standard deviation.

Example 1: Population Variance and Standard Deviation

Question: What is the standard deviation of last year's returns of the 12 funds I have invested in?

At that place is no estimating or forecasting in this job. I am only interested in the 12 funds I have invested in and I don't care about the thousands of other funds which exist in the earth. My population is only these 12 funds. I accept all the information available, every bit it is very easy to detect these 12 funds' functioning data.

I take the performance of each of the 12 funds in the last year, calculate the mean, then the deviations from the mean, square the deviations, sum the squared deviations up, split up by 12 (the number of funds), and go the variance. Then the square root of variance is the standard divergence. In this case, considering I take the information for the whole population available, I call them population variance and population standard difference.

Example ii: Sample Variance and Standard Divergence

Question: What is the standard divergence of last year's returns of equity funds in the world?

Compared to calculating standard deviation of concretely specified 12 funds, I now desire to know the standard deviation of returns of all disinterestedness funds in the world. My population is now much larger than in the previous instance. There are thousands of equity funds in the world. Some of them probably aren't on the Bloomberg, don't have a website, and don't publish their performance. In short, I have no hazard that I could become the data for all the funds. And even if I could, it would take a long time and cost a lot of coin to get all the data.

Opposite to the previous case, I now don't have all the information bachelor and I will take to estimate the population'due south standard deviation from a sample.

Estimating Population Standard Deviation from a Sample

And then how will I exercise it? I will try to collect the information for some of the equity funds ? these funds volition be my sample. It is non necessary (and probably not possible) to collect the data for all the funds in the world (the population). I must but make sure that my sample is large enough. While having the data for 5 funds would probably be insufficient to judge standard departure for the whole population, 100 funds' information can exist plenty and still very realistic to get.

Taking the data for these 100 funds I calculate the variance and standard deviation in the same style equally in example 1 with my 12 funds.

The Departure in Calculation: Population vs. Sample Variance

There is merely one fiddling divergence in the adding of variance and it is at the very finish of it. For both population and sample variance, I calculate the mean, then the deviations from the mean, and then I foursquare all the deviations. I sum all the squared deviations up. Then far it was the aforementioned for both population and sample variance.

When I calculate population variance, I and so divide the sum of squared deviations from the hateful by the number of items in the population (in example 1 I was dividing by 12).

When I calculate sample variance, I dissever it by the number of items in the sample less one. In our example two, I split up by 99 (100 less ane).

As a upshot, the calculated sample variance (and therefore also the standard deviation) will be slightly higher than if we would have used the population variance formula. The purpose of this lilliputian difference it to get a better and unbiased estimate of the population?s variance (by dividing by the sample size lowered by one, we recoup for the fact that we are working only with a sample rather than with the whole population).

In the guide to computing variance and standard deviation we were calculating population variance and standard departure. For sample variance and standard deviation, the only difference is in step four, where we now divide by the number of items less i.

Formulas

Population Variance

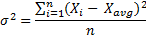
Population variance formula

Population Standard Divergence

Population standard deviation formula

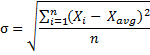
Sample Variance

Sample variance formula

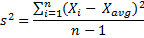
Sample Standard Difference

Sample standard deviation formula

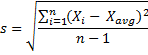
Computing Variance and Standard Deviation in Excel

In Excel, variance and standard difference tin can be easily calculated using the built-in functions: VAR.P, VAR.Due south, STDEV.P, and STDEV.S (of course you lot can also calculate them direct using the formulas to a higher place if you lot like). You can meet how the calculation works in do (as well as the adding of skewness, kurtosis, and other measures) in the Descriptive Statistics Excel Calculator.